精霊の箱1章の面倒な計算について
はじめに
『精霊の箱 上: チューリングマシンをめぐる冒険』の1章でガレットが夕方からやった計算についてまとめておきます。2文字、像に書かれた塔文字の修正された後があり、そこには2通りの文字があるので、2 ** 2の4通りの可能性がありますが、1つは既に誤りであることが分かっている状況です。直して欲しいと主人には頼まれていますが、どのような動作が正しいのか教えて貰えない状況だったので、残りの3つの可能性を全て調べて、一番望ましい動作をする場合を見ないといけなくなりました。1週間のうちの6日までの金貨(0で表現)、と銅貨(1で表現)のならび方は2 ** 6の64通りあります。ガレットは夕方から寝るまでに、次のようになることを確かめました。
1
 この場合が一番厄介です。どんな動作するんですかと言うと、本で言うところの
この場合が一番厄介です。どんな動作するんですかと言うと、本で言うところの11->と00->は普通のプログラミング言語で使える正規表現で言うところの1と0と同じ動作なのでこれに置き換え、1<-は貧者が銅貨を置く動作で、これを¥pとし、0<-は富者が金貨を置く動作で、これを¥rと書くことにします。この設計図の動作を正規表現で書くと次のようになります。
(0|(1(1|0)))*(¥r|(1¥p))
次の表が週の最後の日に像たちがどのように動作をするのかの一覧になります。INが週の最後の日までに置かれた硬貨の配置、OUTが像が動作したあとの硬貨の配置になります。残りの場合の動作についても、設計図とそれに対応する正規表現と表だけ載せております。
| IN | OUT |
|---|---|
| "000000 " | "0000000" |
| "000001 " | "0000011" |
| "000010 " | "0000100" |
| "000011 " | "0000110" |
| "000100 " | "0001000" |
| "000101 " | "0001011" |
| "000110 " | "0001100" |
| "000111 " | "0001111" |
| "001000 " | "0010000" |
| "001001 " | "0010011" |
| "001010 " | "0010100" |
| "001011 " | "0010110" |
| "001100 " | "0011000" |
| "001101 " | "0011011" |
| "001110 " | "0011100" |
| "001111 " | "0011110" |
| "010000 " | "0100000" |
| "010001 " | "0100011" |
| "010010 " | "0100100" |
| "010011 " | "0100110" |
| "010100 " | "0101000" |
| "010101 " | "0101011" |
| "010110 " | "0101100" |
| "010111 " | "0101111" |
| "011000 " | "0110000" |
| "011001 " | "0110011" |
| "011010 " | "0110100" |
| "011011 " | "0110110" |
| "011100 " | "0111000" |
| "011101 " | "0111011" |
| "011110 " | "0111100" |
| "011111 " | "0111111" |
| "100000 " | "1000000" |
| "100001 " | "1000011" |
| "100010 " | "1000100" |
| "100011 " | "1000110" |
| "100100 " | "1001000" |
| "100101 " | "1001011" |
| "100110 " | "1001100" |
| "100111 " | "1001111" |
| "101000 " | "1010000" |
| "101001 " | "1010011" |
| "101010 " | "1010100" |
| "101011 " | "1010110" |
| "101100 " | "1011000" |
| "101101 " | "1011011" |
| "101110 " | "1011100" |
| "101111 " | "1011110" |
| "110000 " | "1100000" |
| "110001 " | "1100011" |
| "110010 " | "1100100" |
| "110011 " | "1100110" |
| "110100 " | "1101000" |
| "110101 " | "1101011" |
| "110110 " | "1101100" |
| "110111 " | "1101111" |
| "111000 " | "1110000" |
| "111001 " | "1110011" |
| "111010 " | "1110100" |
| "111011 " | "1110110" |
| "111100 " | "1111000" |
| "111101 " | "1111011" |
| "111110 " | "1111100" |
| "111111 " | "1111110" |
2
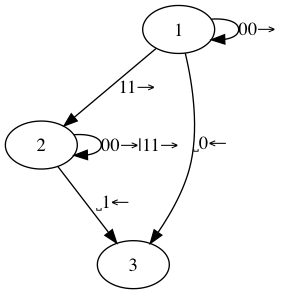
0*((1(0|1)*¥p)|¥r)
| IN | OUT |
|---|---|
| "000000 " | "0000000" |
| "000001 " | "0000011" |
| "000010 " | "0000101" |
| "000011 " | "0000111" |
| "000100 " | "0001001" |
| "000101 " | "0001011" |
| "000110 " | "0001101" |
| "000111 " | "0001111" |
| "001000 " | "0010001" |
| "001001 " | "0010011" |
| "001010 " | "0010101" |
| "001011 " | "0010111" |
| "001100 " | "0011001" |
| "001101 " | "0011011" |
| "001110 " | "0011101" |
| "001111 " | "0011111" |
| "010000 " | "0100001" |
| "010001 " | "0100011" |
| "010010 " | "0100101" |
| "010011 " | "0100111" |
| "010100 " | "0101001" |
| "010101 " | "0101011" |
| "010110 " | "0101101" |
| "010111 " | "0101111" |
| "011000 " | "0110001" |
| "011001 " | "0110011" |
| "011010 " | "0110101" |
| "011011 " | "0110111" |
| "011100 " | "0111001" |
| "011101 " | "0111011" |
| "011110 " | "0111101" |
| "011111 " | "0111111" |
| "100000 " | "1000001" |
| "100001 " | "1000011" |
| "100010 " | "1000101" |
| "100011 " | "1000111" |
| "100100 " | "1001001" |
| "100101 " | "1001011" |
| "100110 " | "1001101" |
| "100111 " | "1001111" |
| "101000 " | "1010001" |
| "101001 " | "1010011" |
| "101010 " | "1010101" |
| "101011 " | "1010111" |
| "101100 " | "1011001" |
| "101101 " | "1011011" |
| "101110 " | "1011101" |
| "101111 " | "1011111" |
| "110000 " | "1100001" |
| "110001 " | "1100011" |
| "110010 " | "1100101" |
| "110011 " | "1100111" |
| "110100 " | "1101001" |
| "110101 " | "1101011" |
| "110110 " | "1101101" |
| "110111 " | "1101111" |
| "111000 " | "1110001" |
| "111001 " | "1110011" |
| "111010 " | "1110101" |
| "111011 " | "1110111" |
| "111100 " | "1111001" |
| "111101 " | "1111011" |
| "111110 " | "1111101" |
| "111111 " | "1111111" |
3

((1+0)|0)*((1+¥p)|¥r)
| IN | OUT |
|---|---|
| "000000 " | "0000000" |
| "000001 " | "0000011" |
| "000010 " | "0000100" |
| "000011 " | "0000111" |
| "000100 " | "0001000" |
| "000101 " | "0001011" |
| "000110 " | "0001100" |
| "000111 " | "0001111" |
| "001000 " | "0010000" |
| "001001 " | "0010011" |
| "001010 " | "0010100" |
| "001011 " | "0010111" |
| "001100 " | "0011000" |
| "001101 " | "0011011" |
| "001110 " | "0011100" |
| "001111 " | "0011111" |
| "010000 " | "0100000" |
| "010001 " | "0100011" |
| "010010 " | "0100100" |
| "010011 " | "0100111" |
| "010100 " | "0101000" |
| "010101 " | "0101011" |
| "010110 " | "0101100" |
| "010111 " | "0101111" |
| "011000 " | "0110000" |
| "011001 " | "0110011" |
| "011010 " | "0110100" |
| "011011 " | "0110111" |
| "011100 " | "0111000" |
| "011101 " | "0111011" |
| "011110 " | "0111100" |
| "011111 " | "0111111" |
| "100000 " | "1000000" |
| "100001 " | "1000011" |
| "100010 " | "1000100" |
| "100011 " | "1000111" |
| "100100 " | "1001000" |
| "100101 " | "1001011" |
| "100110 " | "1001100" |
| "100111 " | "1001111" |
| "101000 " | "1010000" |
| "101001 " | "1010011" |
| "101010 " | "1010100" |
| "101011 " | "1010111" |
| "101100 " | "1011000" |
| "101101 " | "1011011" |
| "101110 " | "1011100" |
| "101111 " | "1011111" |
| "110000 " | "1100000" |
| "110001 " | "1100011" |
| "110010 " | "1100100" |
| "110011 " | "1100111" |
| "110100 " | "1101000" |
| "110101 " | "1101011" |
| "110110 " | "1101100" |
| "110111 " | "1101111" |
| "111000 " | "1110000" |
| "111001 " | "1110011" |
| "111010 " | "1110100" |
| "111011 " | "1110111" |
| "111100 " | "1111000" |
| "111101 " | "1111011" |
| "111110 " | "1111100" |
| "111111 " | "1111111" |
終わりに
ガレットが1章で動作について説明しているところがあります。僕も、そのような表現でこの2つの像の動作を理解しようとしましたが、なかなか難しかったです。妥協して、正規表現で表現することにしました。普段から見るもので慣れているってだけかもしれませんが、この方が僕には分かりやすかったです。